Greetings from 2024! I can't believe this website is still up.
an inclusive and diverse safe space to share screens, videos, and chat about MapleStory.
No ads, no tracking, and no tolerance for hate and discrimination.
I look into this void. I wonder if anyone sees me, or even remembers me...
heyyyyyyyyyyyyyy soooo, kinda random, but decided to try anyways, i'm looking for the nx items Baby Doll Linka (F) & Yui's Wings in Bera, if anyone has it or can pass the msg along to older maple players who might have played in 2014, PLEASEEE LET ME KNOW :sob:

I am Lucavi! I am a veteran! ... I am one of few I am among those who are the last of my kind. . . . I have seen the world of Maple at its most basic! I have seen prices that did not exceed 250K at most I have seen a Maple world without the FM &
wanting to buy a nine-tail fox cape in bera . i cant seem to find one
needing a wife in bera :(
i miss the market on this site a little bit :(
mr. basil iirc you were a jett. just curious if you heard about jetts being removed from the game and if you were going to bother going through the job transfer process before the deadline hits and you become a beginner
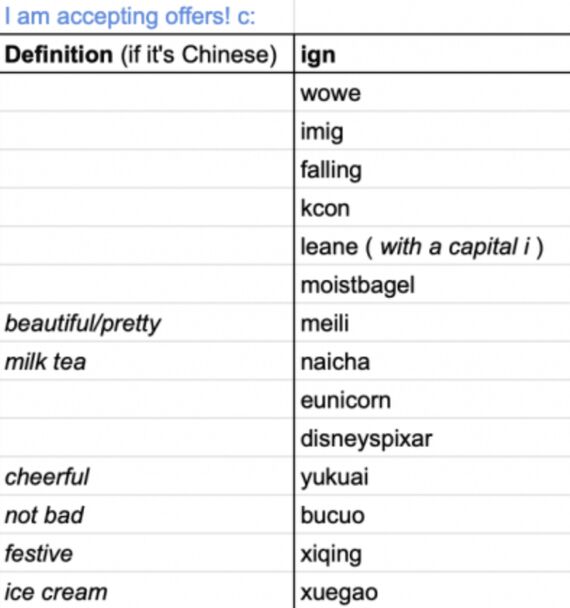
hihi !! idk if anyone still uses this LOL but in case anyone does: i'm getting rid of some igns !! pls take them away disc: eunichi
Let me be the next to scream into the void. Every day I go home from work; a piece of my soul taken from me by my crappy high paying job that I hate. The money coming in is good and I don't at all struggle to pay bills. But work is just draining me of my soul each and every day, turning me into a zombie inside. I just don't want to have to keep doing it for another 34 years until retirement. Man I wish I could just go back to the days where I could just log into maple and mindlessly grind for hours on end without giving a damn about the real world. Anyway how's your life going?
Tuffghost here. I miss /6/. I have found other online communities that fill the void, but basil still has my heart. I met one person irl via basil a long time ago. Thank you based god.
Hello from the future. Who would've thought that this old shell of a website would still be here. I knew a day would come where no one was left but a few people, every once in a while, screaming into the void. I am now one of those people. Ahhhh!
Was everything from the old basilmarket removed? :( I do miss the interactivity of the platform! The other day, I remembered how we had to verify people's legitimacy in selling NX by whispering "trustworthy" and high-leveled individuals from well known guilds! It just made me realize that even as a 15 year old, we were exposed to some pretty complex social conventions in the virtual world of MapleStory... even having "tracks" to find out who's inside a PQ and using autoclickers just to get into them... Crazy times those were!! ;)
Buying Emerald Earrings Scania Active
Happy 2023 guys. Wish this site wasn't so messed up. ktempo/opmeT/TheMuffinLover/whatever other account names got banned over the last 14 years
Logged on MapleStory the other day, remembered this site. Managed to log back in, and alas, here I am. Basilmarket.. greetings from 2023~!! Hey yall~